Эта глава освещает более продвинутые статистические понятия, чем остальные главы, но мы бы хотели начать с небольшого введения в преобразования данных на случай, если вы с ними столкнетесь. Если вам необходимо самостоятельно преобразовать данные, больше информации вы найдете в приложении «Ресурсы».
Когда вы снимаете цифровые фото, иногда получаются фотографии, на которых сложно разглядеть отдельные детали. Возможно, цвета слишком темные или слишком светлые, фото расплывчатое или объекты на изображении слишком маленькие, и вы хотели их приблизить. Вы можете загрузить фото в Instagram или Photoshop и, обработав, сделать его более четким и понятным.
Иногда нам нужно преобразовать и данные. Вы можете получить базу данных и визуализировать ее «как есть», и на вашей визуализации будут части, которые сложно разглядеть. Кроме того, если вы собираетесь сделать статистическое тестирование данных, многие традиционные тесты делают определенные предположения о распределении данных (например, что данные распределены нормально). В реальности, мы часто сталкиваемся с данными, которые не соответствуют этим предположениям. Преобразования данных помогут справиться с обеими этими проблемами. Здесь мы рассмотрим некоторых наиболее распространенные преобразования, чтобы столкнувшись с этими терминами в будущем, вы понимали, что сделали с данными.
Преобразования данных − одна из распространенных процедур обработки, способная обнаружить характерные особенности, скрытые в данных и не видимые в их оригинальной форме. Мы можем преобразовать распределение данных, чтобы видеть их лучше, и чтобы соответствовать любым требуемым предпосылкам статистических тестов. Обычно мы делаем это, заменяя одну переменную математической функцией от этой переменной. Например, вы можете заменить переменную х логарифмом х или квадратным корнем из х.
Никогда не осуществляйте преобразования данных в исходном файле! Либо создайте дополнительную колонку для хранения новых значений каждой переменной, которую вы преобразовываете, либо сделайте копию всего набора данных.
Нормальное распределение и асимметрия данных
Одна из наиболее часто встречающихся предпосылок статистических тестов заключается в том, что данные должны быть нормально распределены. Возможно, вы слышали о нормальном распределении, известном как “колоколообразная (гауссова) кривая”; название кривой связано с тем, что нормальное распределение имеет форму колокола, где данные распределены вокруг центрального значения. Некоторые примеры данных, которые обычно следуют нормальному распределению, связаны с измерениями человека, такими как рост, вес, продолжительность жизни и результаты тестов IQ.
В отличие от нормального распределения, которое располагается симметрично вокруг среднего значения, асимметричные данные, как правило, имеют больше отметок с левой или с правой стороны. У данных, смещенных вправо, длинный хвост тянется вправо от среднего значения, а у данных, смещенные влево, хвост тянется влево. Когда данные сильно скошены, увидеть предельные значения на визуализации может быть сложно. Если вы заметите, что распределение ваших данных смещено, об их трансформации можно думать, если вы делаете статистическое тестирование или данные сложно визуализировать в их оригинальном состоянии.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
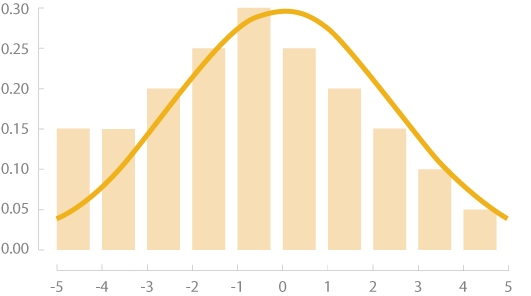
СМЕЩЕНИЕ ВЛЕВО
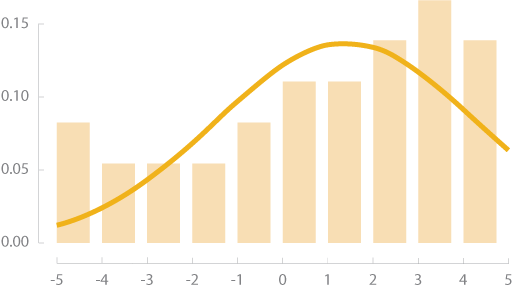
СМЕЩЕНИЕ ВПРАВО
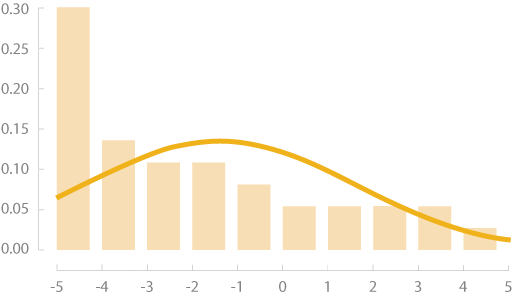
Знакомство с преобразованиями на примере реальных данных
Давайте возьмем численность населения и площадь пятидесяти штатов США и посмотрим, как работают преобразования на реальных данных. Первый шаг в преобразовании − оценить распределение данных. Затем можно принимать решение, какая трансформация будет уместна (если она вообще нужна). Мы можем начать с построения гистограммы данных о населении и графика рассеивания данных о населении и площади, чтобы лучше понять, как они распределены.
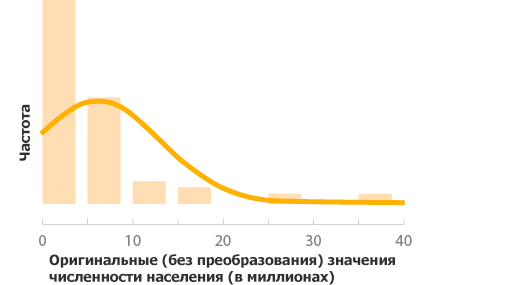
Эта гистограмма показывает, что распределение значений численности искажено вправо. Этого следовало ожидать, поскольку население большинства штатов находится в диапазоне 1-10 миллионов. Если мы хотим сделать статистическое тестирование, которое опирается на предпосылку нормального распределения, эти данные придется преобразовать.
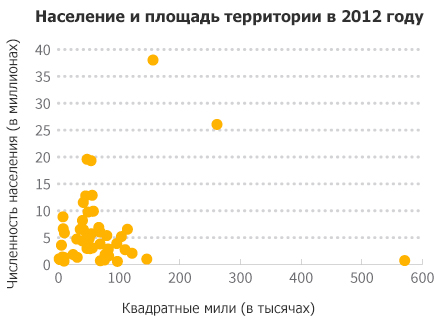
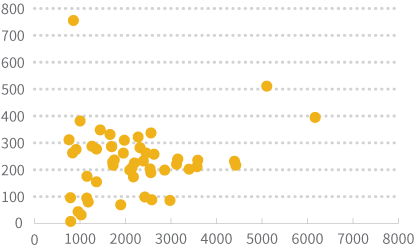
На этом графике рассеивания вы видите, что большинство точек скопилось в нижнем левом углу, усложняя понимание того, как связаны между собой население и территория. Мы не можем просто изменить масштаб графика, чтобы приблизить этот угол, потому что тогда мы лишимся Калифорнии и Аляски. Тем не менее, чтобы упростить просмотр данных, мы можем использовать преобразования.
Существует много методов преобразования, применимых в этих ситуациях, но давайте взглянем на парочку самых традиционных, чтобы увидеть, как они могут повлиять и на визуализацию, и на форму распределения.
ЛОГАРИФМИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ
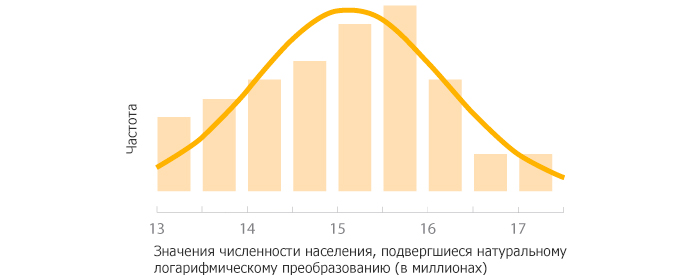
Чтобы осуществить логарифмическое преобразование, вы вычисляете логарифм каждого значения в наборе данных и используете эти преобразованные данные вместо исходных. Логарифмические преобразования оказывают существенный эффект на форму распределения, и могут в визуализациях приблизить крайние выбросы к остальным данным, и графики выглядят не такими растянутыми. Вы можете использовать натуральные или десятичные логарифмы. Ниже вы видите гистограмму данных о населении после применения натурального логарифмического преобразования, а также график рассеивания населения и площади территории после такого же преобразования.
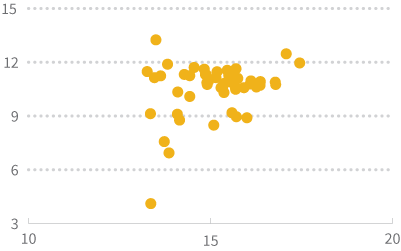
ПРЕОБРАЗОВАНИЕ КВАДРАТНОГО КОРНЯ
Преобразование квадратного корня использует квадратный корень каждого значения вместо логарифма, и оказывает более умеренный эффект на форму распределения. Два следующих графика показывают гистограмму данных численности населения и график рассеивания населения по территории после применения преобразования квадратного корня.
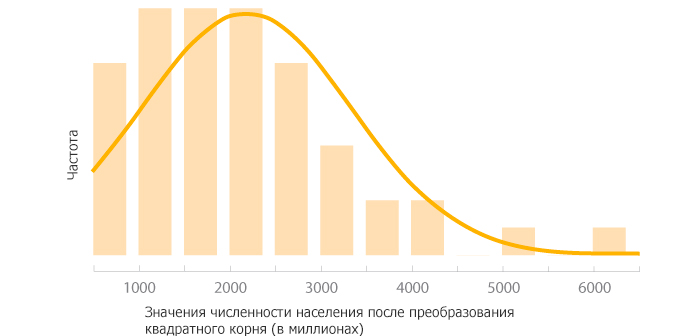
Выбор правильного преобразования
Когда вы станете лучше разбираться в различных методах преобразования, у вас может возникнуть вопрос, как выбирать между ними. Ответ на него не прост, и хотя существуют формальные статистические методы для выбора преобразования, нам часто приходится применять метод проб и ошибок в сочетании с пониманием различных преобразований. Общая стратегия заключается в том, чтобы применить некоторые из наиболее используемых преобразований, таких как логарифмы, квадратный корень, квадрат, обратная дробь и корень кубический, и затем выбрать лучший, исходя из полученных результатов.
Судя по преобразованным гистограммам выше, логарифмическое преобразование данных подошло лучше – данные распределены нормально, в то время как данные, преобразованные квадратным корнем, все еще смещены вправо. Так что в этом примере, если вы делаете статистический тест, допускающий, что данные распределены нормально, метод логарифмического преобразования подойдет больше, чем квадратный корень.
С другой стороны, если ваша основная цель в этом примере − визуализация соотношения между численностью населения штата и его площадью, то преобразование квадратного корня лучше разносит данные, делает их более наглядными, чем логарифмическое преобразование.
Распространенные преобразования
| Метод | Математическая операция | Подходит для: | Не подходит для: |
| Логарифм | ln(x) log10(x) | Данных, смещенных вправо | Нулевых значений |
| Квадратный корень | √x | особенно хорошо работает со степенями 10 более высокого порядка (например, 1000, 100000) | Отрицательных значений |
| Квадрат | x² | Данных, смещенных вправо | Отрицательных значений |
| Корень кубический | x⅓ | Данных, смещенных влево | Отрицательных значений |
| Обратная дробь | 1/x | Данных, смещенных вправо | Не так эффективен при нормализации, как логарифмическое преобразование |
Предостережения о преобразованиях
Поскольку методы преобразования включают в себя применение к вашим данным математических функций, вам следует быть внимательным, представляя или объясняя любые выводы, полученные из преобразованных данных, поскольку преобразование меняет единицу измерения данных. Например, когда мы применяем логарифмическую функцию к переменной численности населения, единицей измерения становится логарифм численности. Когда вы делитесь своими результатами, ваша аудитория может предположить, что полученные вычисления или визуализации основаны на исходных данных, поэтому, если значения были преобразованы, вам следует четко сообщить, какие преобразования были применены, а также в каких единицах отображены данные.
Если вы используете преобразованные данные для вычисления статистических значений, как, например, среднее значение, вам следует совершить обратное преобразование конечных результатов и представить их в изначальных единицах. Для этого вы просто применяете математическую функцию, обратную той, что использовали вначале. Например, если вы применили преобразование квадратного корня, вам следует совершить обратное преобразование путем возведения ваших конечных результатов в квадрат.
Может быть, вы не будете сталкиваться с преобразованиями каждый день, но если это произойдет, полезно знать, почему они были применены и как они повлияют на ваши данные. Важно уметь видеть разные части картины, когда вы работаете с данными, и преобразования дают вам еще один инструмент для этого!
